你好，我是黄申。

之前我使用Boston Housing的数据，阐述了如何使用多元线性回归。可是，计算机系统究竟是如何根据观测到的数据，来拟合线性回归模型呢？这两节，我就从最简单的线性方程组出发，来说说如何求解线性回归的问题。

在第29讲中，我讲过机器学习中两类很重要的方法：回归分析以及线性回归。回归分析属于监督式学习算法，主要研究一个或多个随机变量 \(y\_1\) ， \(y\_2\) ，…， \(y\_i\) 与另一些变量 \(x\_{1}\) ， \(x\_{2}\) ，…， \(x\_{k}\) 之间的关系。其中，我们将 \(y\_{1}，y\_{2}、…，y\_{i}\) 称为因变量， \(x\_1，x\_2，…，x\_k\) 称为自变量。按照不同的维度，我们可以把回归分为三种。

• 按照自变量数量，当自变量 \(x\) 的个数大于1时就是多元回归。

• 按照因变量数量，当因变量 \(y\) 个数大于1时就是多重回归。

• 按照模型种类，如果因变量和自变量为线性关系时，就是线性回归模型；如果因变量和自变量为非线性关系时，就是非线性回归分析模型。

高斯消元法

对于回归分析来说，最简单的情形是只有一个自变量和一个因变量，且它们大体上是有线性关系的，这就是一元线性回归。对应的模型很简单，就是 \(Y=a+bX+ε\) 。这里的 \(X\) 是自变量， \(Y\) 是因变量， \(a\) 是截距，b是自变量的系数。前面这些你估计都很熟悉，最后还有个 \(ε\) ，这表示随机误差，只不过我们通常假定随机误差的均值为 \(0\) 。进一步来说，如果我们暂时不考虑a和ε，把它扩展为多元的形式，那么就可以得到类似下面这种形式的方程：

\(b\_1·x\_1+b\_2·x\_2+…+b\_{n-1}·x\_{n-1} +b\_n·x\_n=y\)

假设我们有多个这样的方程，就能构成线性方程组，我这里列出一个例子。

\(2x\_1+x\_2+x\_3=0\) - \(4x\_1+2x\_2+x\_3=56\) - \(2x\_1-x\_2+4x\_3=4\)

对于上面这个方程组，如果存在至少一组 \(x\_1、x\_2\) 和 \(x\_3\) 使得三个方程都成立，那么就叫方程有解；如果没有，那么我们就说方程无解。如果方程有解，那么解可能是唯一，也可能是多个。我们通常关心的是，方程组是不是有解，以及 \(x\_1\) 一直到 \(x\_n\) 分别是多少。

为了实现这个目的，人们想了很多方法来求解方程组，这些方法看起来多种多样，其实主要就是两大类，直接法和迭代法。

直接法就是通过有限次的算术运算，计算精确解。而迭代法，我们在第3讲就提到过，它是一种不断用变量的旧值递推新值的过程。我们可以用迭代法不断地逼近方程的精确解。

这里，我就从上面这个方程组的例子出发，阐述最常见的高斯消元法，以及如何使用矩阵操作来实现它。

高斯消元法主要分为两步， 消元 （Forward Elimination）和 回代 （Back Substitution）。所谓消元，就是要减少某些方程中元的数量。如果某个方程中的元只剩一个 \(x\_m\) 了，那么这个自变量 \(x\_m\) 的解就能知道了。所谓的回代，就是把已知的解 \(x\_m\) 代入到方程式中，求出其他未知的解。

我们先从消元开始，来看这个方程组。

\(2x\_1+x\_2+x\_3=0\) - \(4x\_1+2x\_2+x\_3=56\) - \(2x\_1-x\_2+4x\_3=4\)

首先保持第一个方程不变，然后消除第二个和第三个方程中的 \(x\_1\) 。对于第二个方程，方法是让第二个方程式减去第一个方程式的两倍，方程的左侧为：

\((4x\_1+2x\_2+x\_3)-2(2x\_1+x\_2+x\_3)=-x\_3\)

方程的右侧变为：

\(56-2·0=56\)

所以第二个方程变为：

\(-x\_3=56\)

这样三个方程式就变为：

\(2x\_1+x\_2+x\_3=0\) - \(-x\_3=56\) - \(2x\_1-x\_2+4x\_3=4\)

对于第三个方程同样如此，我们需要去掉其中的 \(x\_1\) 。方法是让第三个方程减去第一个方程，之后三个方程式变为：

\(2x\_1+x\_2+x\_3=0\) - \(-x\_3=56\) - \(-2x\_2+3x\_3=4\)

至此，我们使用第一个方程式作为参照，消除了第二个和第三个方程式中的 \(x\_1\) ，我们称这里的第一个方程式为“主元行”。

接下来，我们要把第二个方程式作为“主元行”，来消除第三个方程中的 \(x\_2\) 。你应该能发现，第二个方程中的 \(x\_2\) 已经没有了，失去了参照，这个时候我们需要把第二个方程和第三个方程互换，变为：

\(2x\_1+x\_2+x\_3=0\) - \(-2x\_2+3x\_3=4\) - \(-x\_3=56\)

到了这个时候，由于第三个方程已经没有 \(x\_2\) 了，所以无需再消元。如果还有 \(x\_2\) ，那么就需要参照第二个方程式来消除第三个方程中的 \(x\_2\) 。

观察一下现在的方程组，第一个方程有3个自变量，第二个方程有2个自变量，第三个方程只有1个自变量。这个时候，我们就可以从第三个方程开始，开始回代的过程了。通过第三个方程，显然我们可以得到 \(x\_3=-56\) ，然后把这个值代入第二个方程，就可以得到 \(x\_2 = -86\) 。最后把 \(x\_2\) 和 \(x\_3\) 的值代入第一个方程式，我们可以得到 \(x\_1=71\) 。

使用矩阵实现高斯消元法

如果方程和元的数量很小，那么高斯消元法并不难理解。可是如果方程和元的数量很多，整个过程就变得比较繁琐了。实际上，我们可以把高斯消元法转为矩阵的操作，便于自己的理解和记忆。

为了进行矩阵操作，首先我们要把方程中的系数 \(b\_i\) 转成矩阵，我们把这个矩阵记作 \(B\) 。对于上面的方程组示例，系数矩阵为：

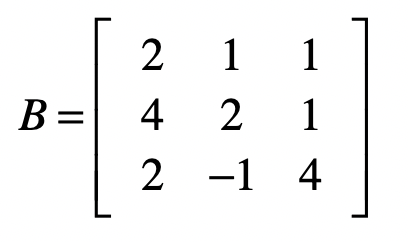
那么，最终我们通过消元，把系数矩阵B变为：

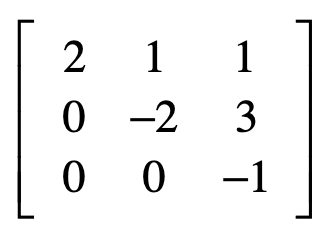
从此可以看出，消元的过程就是把原始的系数矩阵变为上三角矩阵。这里的上三角矩阵表示，矩阵中只有主对角线以及主对角线以上的三角部分里有数字。我们用 \(U\) 表示上三角矩阵。

而回代呢，我们最终得到的结果是：

\(x\_1=71\) - \(x\_2=-86\) - \(x\_3=-56\)

我们可以把这几个结果看作：

\(1·x\_1+0·x\_2+0·x\_3=71\) - \(0·x\_1+1·x\_2+0·x\_3=-86\) - \(0·x\_1+0·x\_2+1·x\_3=-56\)

再把系数写成矩阵的形式，就是：

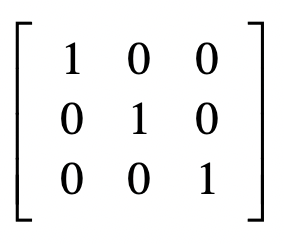
发现没？这其实就是单位矩阵。所以说，回代的过程是把上三角矩阵变为单位矩阵的过程。

为了便于后面的回代计算，我们也可以把方程式等号右边的值加入到系数矩阵，我们称这个新的矩阵为 增广矩阵 ，我把这个矩阵记为 \(A\) 。

好，现在让我们来观察一下这个增广矩阵 \(A\) 。

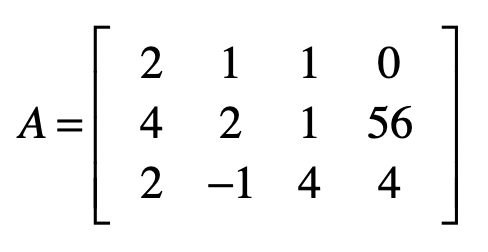
对于这个矩阵，我们的最终目标是，把除了最后一列之外的部分，变成单位矩阵，而此时最后一列中的每个值，就是每个自变量所对应的解了。

之前我已经讲过矩阵相乘在向量空间模型、PageRank算法和协同过滤推荐中的应用。这里，我们同样可以使用这种操作来进行消元。为了方便你理解，我们可以遵循之前消元的步骤一步步来看。

还记得这个方程组消元的第一步吗？对，首先保持第一个方程不变，然后消除第二个和第三个方程中的 \(x\_1\) 。这就意味着要把 \(A\_{2,1}\) 和 \(A\_{3,1}\) 变为 \(0\) 。

对于第一个方程式，如果要保持它不变，我们可以让向量 \(\[1, 0, 0\]\) 左乘 \(A\) 。对于第二个方程，具体操作是让第二个方程式减去第一个方程式的两倍，达到消除 \(x\_1\) 的目的。我们可以让向量 \(\[-2, 1, 0\]\) 左乘 \(A\) 。对于第三个方程式，具体操作是让第三个方程式减去第一个方程式，达到消除 \(x\_1\) 的目的。我们可以让向量 \(\[-1, 0, 1\]\) 左乘 \(A\) 。我们使用这三个行向量组成一个矩阵 \(E1\) 。

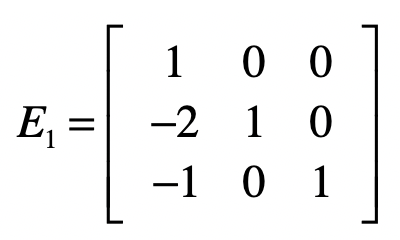
因此，我们可使用下面这个矩阵 \(E1\) 和 \(A\) 的点乘，来实现消除第二个和第三个方程式中 \(x\_1\) 的目的。

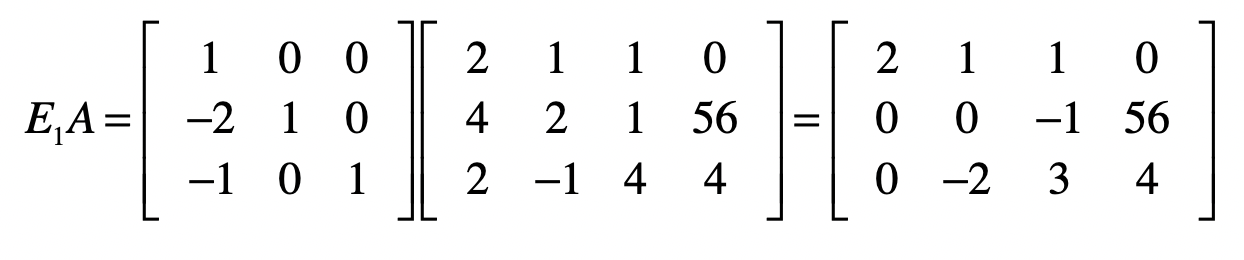
你会发现，由于使用了增广矩阵，矩阵中最右边的一列，也就是方程等号右边的数值也会随之发生改变。

下一步是消除第三个方程中的 \(x\_2\) 。依照之前的经验，我们要把第二个方程式作为“主元行”，来消除第三个方程中的 \(x\_2\) 。可是第二个方程中的 \(x\_2\) 已经没有了，失去了参照，这个时候我们需要把第二个方程和第三个方程互换。这种互换的操作如何使用矩阵来实现呢？其实不难，例如使用下面这个矩阵 \(E2\) 左乘增广矩阵 \(A\) 。

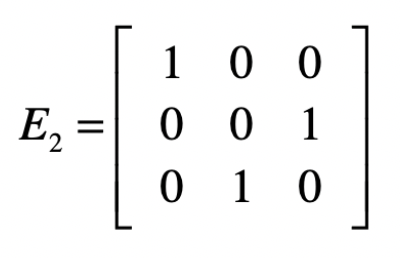
上面这个矩阵第一行 \(\[1 0 0\]\) 的意思就是我们只取第一行的方程，而第二行 \(\[0 0 1\]\) 的意思是只取第三个方程，而第三行 \(\[0 1 0\]\) 表示只取第二个方程。

我们先让 \(E1\) 左乘 \(A\) ，然后再让 \(E2\) 左乘 \(E1A\) 的结果，就能得到消元后的系数矩阵。

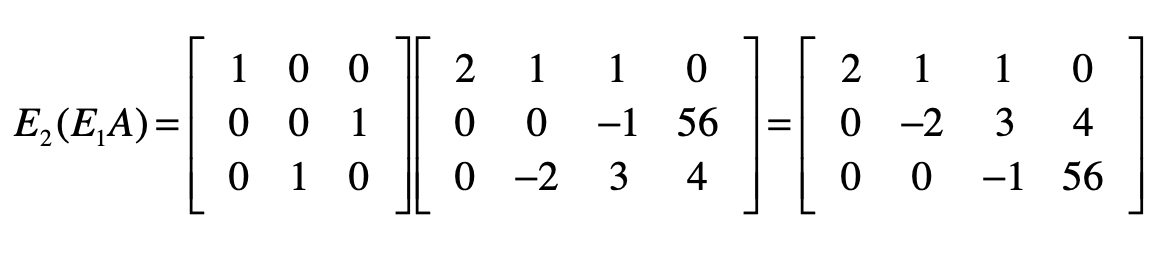
我们把 \(E1\) 点乘 \(E2\) 的结果记作 \(E3\) ，并把 \(E3\) 称为消元矩阵。

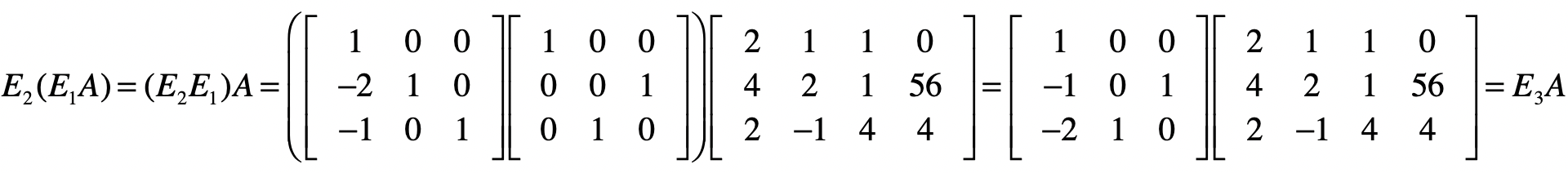
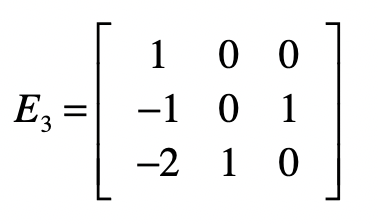
对于目前的结果矩阵来说，除了最后一列，它已经变成了一个上三角矩阵，也就是说消元步骤完成。接下来，我们要使得最后一列之外的部分变成一个单位矩阵，就能得到最终的方程组解。和消元不同的是，我们将从最后一行开始。对于最后一个方程，我们只需要把所有系数取反就行了，所以会使用下面这个矩阵 \(S1\) 实现。

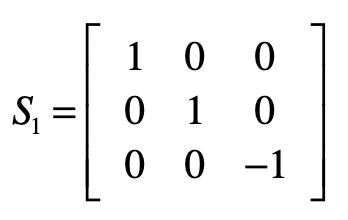
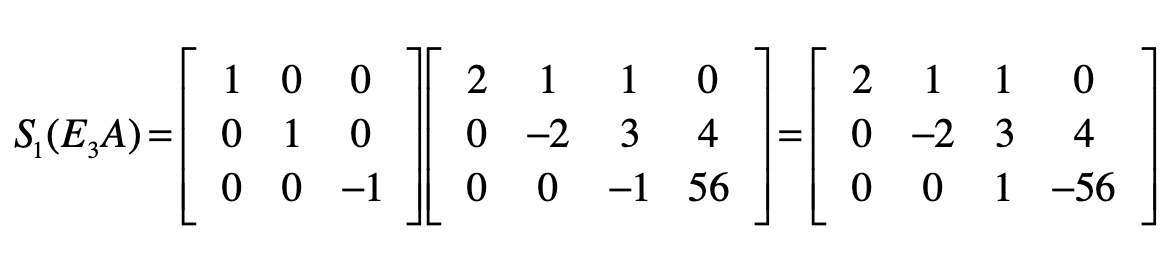
接下来要去掉第二个方程中的 \(x\_3\) ，我们要把第二个方程减去3倍的第三个方程，然后除以-2。首先是减去3倍的第三个方程。

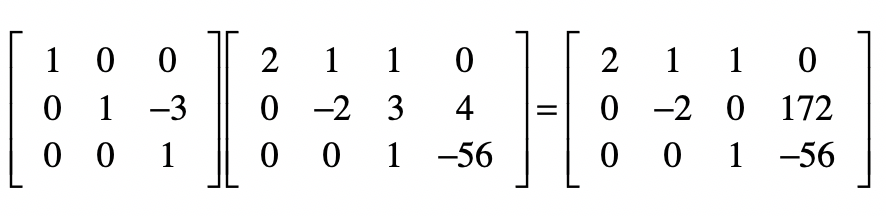
然后把第二个方程除以-2。

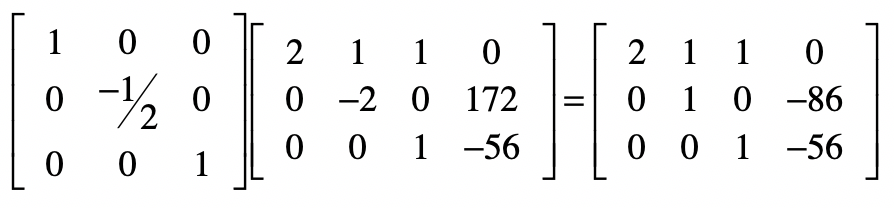
最后，对于第一个方程，我们要把第一个方程减去第二个和第三个方程，最后除以2，我把这几步合并了，并列在下方。

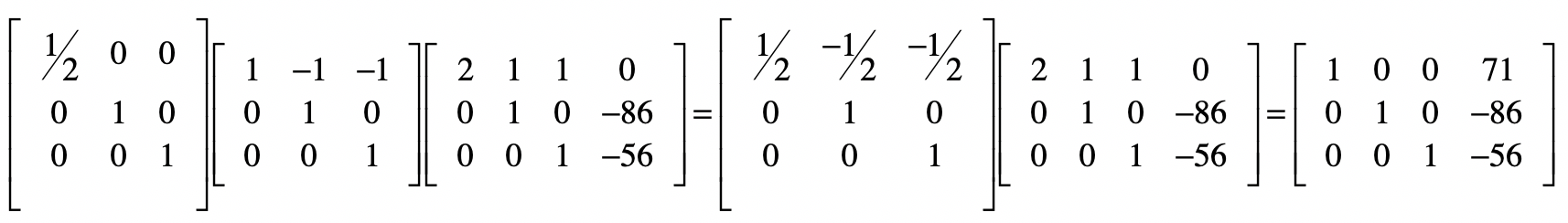
最终，结果矩阵的最后一列就是方程组的解。我们把回代部分的矩阵，都点乘起来。

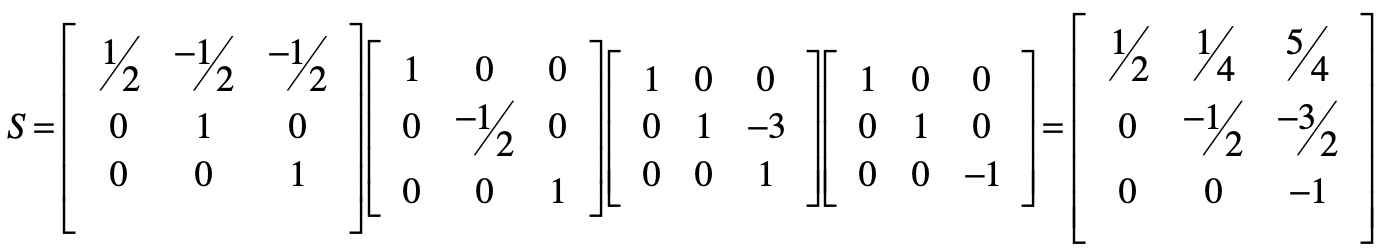
而消元矩阵 \(E3\) 为：

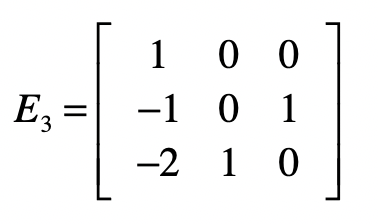
我们可以让矩阵 \(S\) 左乘矩阵 \(E3\) ，就会得到下面的结果。

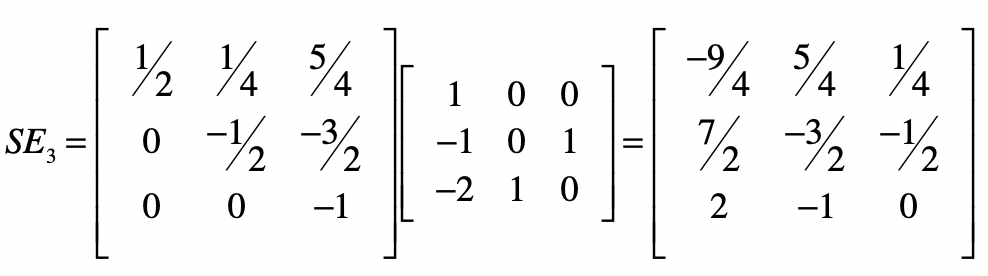
我们把这个矩阵记作 \(SE\) ，把乘以最初的系数矩阵 \(B\) ，就得到了一个单位矩阵。根据逆矩阵的定义， \(SE\) 就是 \(B\) 的逆矩阵。换个角度来思考，使用消元法进行线性方程组求解的过程，就是在找系数矩阵的逆矩阵的过程。

总结

今天我们一起探讨了求解线性方程组最常见的方法之一，高斯消元法。这个方法主要包含了消元和回代两个步骤。这些步骤都可以使用矩阵的操作来进行。从矩阵的角度来说，消元就是把系数矩阵变为上三角矩阵，而回代是把这个上三角矩阵变为单位矩阵。我们可以直接把用于消元和回代的矩阵，用于由系数和因变量值组成的增广矩阵，并获得最终的方程解。

线性方程组的概念，也是线性回归分析的基础。在线性回归时，我们也能获得由很多观测数据值所组成的方程组。但是，在进行线性回归分析时，方程组的处理方式和普通的方程组求解有一些不同。其中有两个最主要的区别。

第一个区别是，在线性回归分析中，样本数据会告诉我们自变量和因变量的值，要求的是系数。而在线性方程组中，我们已知系数和因变量的值，要求的是自变量的值。

第二个区别是，在线性回归分析中，方程的数量要远远大于自变量的数量，而且我们不要求每个方程式都是完全成立。这里，不要求完全成立的意思是，拟合出来的因变量值可以和样本数据给定的因变量值存在差异，也就允许模型拟合存在误差。模型拟合的概念我在上一模块的总结篇中重点讲解了，所以你应该能理解，模型的拟合不可能100%完美，这和我们求解线性方程组精确解的概念是不同的。

正是因为这两点差异，我们无法直接使用消元法来求解线性回归。下一节，我会来详细解释，如何使用最小二乘法来解决线性回归的问题。

思考题

请分别写出下面这个方程组的消元矩阵和回代矩阵，并求出最终的解。

\(x\_1-2x\_2+x\_3-4x\_4=4\) - \(x\_2-x\_3+x\_4=-3\) - \(x\_1+3x\_2+x\_4=1\) - \(-7x\_2+3x\_3+x\_4=-3\)

欢迎留言和我分享，也欢迎你在留言区写下今天的学习笔记。你可以点击“请朋友读”，把今天的内容分享给你的好友，和他一起精进。